총평
무난무난한 Div2. 근데 내 실력은 다사다난한듯..
대회 후기

6058점. 위에 복붙충 2명 빼면 30등. C만 제대로 했으면 한 500점은 더 받았겠다 ㅋㅋ;
A는 A였다.
B가 생각보다 어려워서 당황했다. 구현을 이상하게 해서 푸는 데 좀 걸림.
C를 보고 나서 풀이는 금방 나왔는데.. 왠지 모르게 계~~속 틀렸다. 중간에 틀린 거 몇 개 찾아서 고쳤는데도 계속 틀리길래 망했다 하고 일단 D로 도망갔다.
D가 easy/hard로 나뉘어 있었는데, easy는 대충 하면 돼서 대충 짜서 냈다. 그런데 hard는 대충 하면 안 돼서 생각보다 한참 걸렸다. C를 못 푼 상태라서 마음이 급해서 더 오래 걸린 거 같다. 막상 짜고 보니 코드는 또 별로 안 길었다.
E를 봤는데 얘는 또 풀이가 바로 생각나서 풀었다. 그리고 나서 드디어 C에 한 뻘짓을 발견하고 C도 맞았다.
F는 남은 시간 안에는 못 푸는 문제였다.
문제별 풀이
A
\( a \mod b \le [\frac{a-1}{2}] \) 가 성립하므로, 답은 아무리 커 봐야 \( [\frac{r-1}{2}] \) 이다. a = r, b = \( [\frac{r}{2}] + 1 \) 로 설정하면 이 답을 달성할 수 있으므로, 만약 l이 충분히 작다면 \( [\frac{r-1}{2}] \) 이 답이 된다.
그렇지 않다면, l이 \( [\frac{r}{2}] + 1 \)보다 크다는 뜻이므로 a mod b = a-b가 항상 성립한다. 이 때의 답은 r-l이 된다.
코드 : http://codeforces.com/contest/1562/submission/127586156
B
예제를 열심히 관찰하다 보면, 답이 그렇게 크지 않을 것임을 짐작할 수 있다. 그래서 n이 50이고 t가 1000이니까 대충 답이 3 이하인 경우를 다 해 보는 코드를 내면 맞는다.
사실, 답은 항상 2 이하이다. 답이 1이 아니려면 모든 자릿수가 2, 3, 5, 7로만 이루어져 있어야 하는데 어떻게 수가 주어져도 다음 목록에서 적어도 하나를 찾을 수 있다 : {22, 25, 27, 32, 33, 35, 52, 55, 57, 72, 75, 77} (53 같이 어떻게 지워도 소수만 남는 수는 안 주어진다는 조건 때문이다.)
코드 : http://codeforces.com/contest/1562/submission/127586655
C
문자열에서 '0'의 위치에 주목해 보자. 0이 발견된 위치를 i라고 할 때, 두 가지 케이스에 대해 답을 찾을 수 있다.
1) i가 문자열의 앞 절반에 해당 : [i, n]과 [i+1, n]의 값이 같다. i가 문자열의 앞 절반이므로 길이 조건도 만족.
2) i가 문자열의 뒤 절반에 해당 : [1, i]의 값은 [1, i-1]의 값의 2배이다. 역시 길이 조건 만족.
만약 문자열에 0이 없다면 "111...1"이라는 뜻이므로 [1, n-1], [2, n] 이런 식으로 골라주면 된다.
+ 나는 문자열에 0이 없을 때 [1, n-1], [1, n]이 답인 줄 알고 1시간 넘게 삽질했다.. 여러분은 제발 안 그러길 바란다.
코드 : http://codeforces.com/contest/1562/submission/127590758
D
(D1) 문자열에서 짝수 번째 문자를 다 뒤집었다고, 즉 '+' -> '-', '-' -> '+'로 바꾸었다고 하면 각 쿼리에서 묻는 것은 "구간의 + 개수와 - 개수가 같도록 제거해야 되는 최소 문자 수"이다. 여기서 유의할 점이, 문자를 하나 제거하면 홀짝성이 바뀌어서 그 문자 오른쪽이 다 뒤집혀야 한다는 것이다. 예를 들어, 짝수 번째 문자를 다 뒤집은 상태가 "+--+-+"이고 여기서 3번째 문자인 '-'를 제거했다고 하면 "+--+-"이 되는 것이다.
어쨌든, 이제 예제를 관찰하다 보면 답이 "(+ 개수) = (- 개수)일 경우 0, 아닐 경우 (문자열 길이가 홀수면 1, 짝수면 2)) 라는 추측을 할 수 있다. 여기까지만 생각하고 그대로 짜서 내면 D1을 맞을 수 있다.
(D2) 이제 무슨 문자를 제거해야 하는지까지 출력해야 하기 때문에, "왜 답이 그렇게 되느냐?"에 대해서 생각을 해 보아야 한다.
우선 문자열 길이가 짝수이(고 답이 0이 아니)면 구간에서 맨 뒤 문자를 제거해서 길이가 홀수인 상황으로 만들 수 있다. 이제 우리는 문자를 딱 하나 제거해서 구간의 +와 - 개수를 똑같이 만들면 된다.
구간에서 (+ 개수) - (- 개수)의 prefix sum을 생각하자. 구간 전체에서 (+ 개수) - (- 개수)를 S라고 하면, 대충 prefix sum이 "S의 절반"쯤 되는 지점에서 문자를 제거하면 그 뒤로는 +와 -가 뒤집히므로 개수가 같아질 것이라고 일단 생각할 수 있다. 정확히 어디 있는 문자를 제거해야 하는지 알기 위해서는 예제를 하나 갖고 오면 좋다.
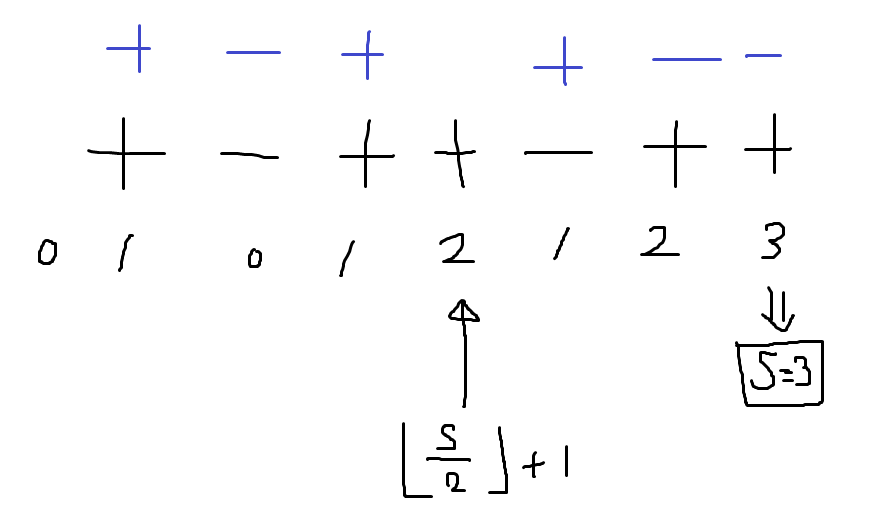
prefix sum이 \( [\frac{S}{2}] + 1 \)이 되는 "최초의" 위치를 찾으면 거기 있는 문자는 반드시 '+' 이다. 이제 그 문자를 제거하게 되면 앞쪽에서는 +가 \( [\frac{S}{2}] \)개 더 많고 뒤쪽에서는 원래 +가 \( S - ( [\frac{S}{2}] + 1) = [\frac{S}{2}] \) 개 더 많아서 (S가 홀수이므로 성립) 뒤쪽의 +-를 뒤집으면 개수가 똑같아진다.
위 예제는 S가 양수임을 가정했는데, S가 음수이면 (- 개수) - (+ 개수)의 prefix sum에 대해 비슷한 논리를 적용하면 -(abs(S) / 2 + 1)에 해당하는 위치를 찾으면 된다. 자세한 구현 방법은 코드를 참고.
코드(D1) : http://codeforces.com/contest/1562/submission/127588234
코드(D2) : http://codeforces.com/contest/1562/submission/127589665
E
가장 핵심이 되는 관찰은 "어떤 [s, e] 부분문자열을 먹기로 했으면, [s, e+1], [s, e+2], ..., [s, n]까지 무조건 다 먹는 것이 이득이다" 라는 것이다. 일단 저렇게 먹으면 사전순 조건은 당연히 만족하고, 거기에 더해 중간에 먹다 말고 다른 데로 넘어갔다면 LIS의 길이를 줄이지 않으면서 그런 부분을 없앨 수 있다는 사실을 증명할 수 있다.
(증명) [s, e], [s, e+1], ..., [s, k]까지 먹고 바로 다음에 s < s'인 [s', e']을 먹었다고 하자. 이는 [s', e']가 [s, k]보다 사전 순으로 뒤에 있음을 의미한다.
만약 [s', e']가 [s, k]를 prefix로 포함하지 않으면, [s, k+1]부터 [s, n]에 해당하는 문자열 역시 [s', e']보다 사전 순으로 앞에 있다는 뜻이므로 걔네들까지 다 먹는 것이 무조건 이득이다.
그게 아니라면, 즉 [s', e']이 [s, k]를 prefix로 포함한다면 [s, e], [s, e+1], ..., [s, k] 각각에 대해 그것과 동일한 [s', a'], [s', a'+1], ..., [s', a' + (k - e)]가 존재하므로 [s, e], ..., [s, k]를 먹은 대신 [s', a'], ..., [s', a' + (k - e)]를 먹었다고 해도 LIS의 길이가 똑같다.
이런 식으로 반복하다 보면 언젠가는 "중간에 먹다 말고 넘어간" 부분이 없어질 것이므로 증명이 완료된다.
이제, DP[s] : (마지막으로 [s, e], ..., [s, n]을 먹은 시작점을 s라고 할 때, LIS의 길이) 라고 정의하면 s<s'인 DP[s] -> DP[s']으로 값을 넘겨 줄 때 "[s, n]까지 먹고 다음 시작점을 s'로 한다고 했을 때 가장 먼저 먹을 수 있는 [s', e']", 즉 [s, n] < [s', e']인 e'의 최솟값을 구해서 DP[s'] = max(DP[s'], DP[s] + (n - e' + 1)) 로 갱신을 해 주면 된다.
앞에서 말한 e'을 O(1)에 구해야 DP 값을 O(N^2)에 구할 수 있다. 이것은 O(N^2)으로 LCP(Longest Common Prefix) 전처리를 해 놓으면 s와 s'의 LCP 바로 다음 위치를 비교하는 것으로 바로 구할 수 있다.
코드 : http://codeforces.com/contest/1562/submission/127590523
F
추가예정.
일단 어려워 보이긴 함
'알고리즘 > 온라인 대회' 카테고리의 다른 글
| Codeforces Round #804 (0) | 2022.07.05 |
|---|---|
| Codeforces Round #742 (0) | 2021.09.28 |
| Codeforces Deltix Round, Summer 2021 (0) | 2021.09.05 |
| 제 3회 소프트콘 후기 (0) | 2021.08.29 |
| Codeforces Round #737 (0) | 2021.08.23 |